When Models See Ghosts - Investigating Why Adversarial Examples Break Our Models
Explore the trade-offs between accuracy, simplicity, and the chaos of high-dimensional data.
Howdy 🤠! This blog is my attempt at unpacking why adversarial examples exist and at piecing together why models are often wrong almost everywhere. I've spent an unhealthy number of hours reading arXiv papers (and should probably spend hundreds more). I'm not claiming this is the gospel truth. I've put together what makes sense to me & I'll do my best to explain manifolds, dimensions, dimples, and a bunch of other data geometry stuff as clearly as I can.
I've sat on publishing this for ~4 months now 🫠. Truth is, I feel awkward posting something like this in a field that's academically published this much. There's a constant flow of new defenses & research that shakes up how everyone thinks these systems work (Robbinson et al., 2025 😅). I wrote this back in late January & A LOT has changed since then. I want to emphasize that there's no single explanation that captures it all & not everyone sees it the same way. Consider this a snapshot in time of how I and perhaps others understand these vulnerabilities.
NOTE: This blog provides an overview of the broader field, drawing on the work of many others. I've chosen to emphasize concepts rather than a full history of who did what. I don’t have the luxury of 2,000 GPUs💔 while I've been able to make certain observations independently and through collaboration, I recognize that my understanding of these ideas has been shaped & influenced by the research of many people.
I don't have any real academic education or a PhD. Expect that I might abstract and oversimplify certain concepts. If for some reason this blog upsets you, refer to my Content Policy. I've included a messy/unsorted list of reading materials that have taught, shaped, and challenged my understanding → here.
I read a few papers a week. The best way I've found to stay up-to-date with the right arXiv papers is with Dreadnode's Paperstack instance. I find it better than setting up/using arxival, pasa, etc. It's free, I love it, and you might like it too.
I wanna pitch my 2¢ on issues we're collectively trying to fix & paint how I view the industry. For starters, I think adversarial machine learning (AML) is becoming chaotic and hard to follow. We're in this publishing gold rush, and I believe there's a huge gap between what researchers are chasing & defenses that actually work in real-world production environments. To rub salt in the wound, every week new papers claim breakthrough defenses only to be broken that same week. It's a bit of a mess 😅, but if you take a step back, you'll realize that we're all trying to answer the same question:
How can we rely on unreliable models and still build systems that are secure?
Given how we've chosen to deploy models within our applications, I'm damn well certain robustness alone won't save us. Ideally, we want to reach a point where we can guarantee that even if a model misclassifies something, the system won't go ahead and perform a misguided action. I truly believe that through collective efforts, shared knowledge, & by building on each other's work rather than just racing to publish on academic clusters, we'll get there.

I'm assuming you have some foundational knowledge & a rough understanding of how models work, learn, optimize, and predict. If you need a refresher, this excellent video by Andrej Karpathy provides a good overview.
From image recognition to natural language processing, we tend to think of machine learning models as having impressively high accuracy (Krizhevsky et al., 2012; He et al., 2016; Devlin et al., 2019; Jumper et al., 2021). They do... and it's undeniably extremely impressive, but their success often largely rides on the fact that these benchmark tasks recycle the same kinds of naturally occurring data they were trained on to begin with. You can easily flip the script & oftentimes trivially make them classify incorrectly and look unaligned. We'll specifically be looking at adversarial examples (Szegedy et al., 2014; Biggio et al., 2017), which are often mathematically optimized changes (perturbations) to an input crafted by an adversary to trick a model into making a misclassification.

LLM are systems that learn from vast amounts of text, books, websites, and code to understand and generate language. This learned text data doesn't fill the entire space of all possible sequences of words or characters, which is incredibly high-dimensional (all possible inputs) and vast. Instead, meaningful sentences that make sense, follow grammar, or convey broad ideas (feature space) form a much smaller structure called a manifold.
The feature space manifold is "shaped" by the patterns of the training data. This is influenced by the data itself (different domains & over/underrepresented regions) and the model’s ability to process inputs. Models rely on the manifold (in the feature space) to process inputs and make predictions as they learn patterns from the training data's manifold. Rightly or wrongly, we can think of this as being where models derive it's "knowledge".
At a high level, adversarial examples work because they exploit the gap between the statistical patterns a model captures and the semantic features we'd as humans would expect them to learn (statistical correlations vs meaningful features). When models are trained, they learn to map this input space (the raw data) to feature space (internal representations) on some low-dimensional manifold. This happens because models love sparcity. So even though our real world data is high-dimensional theres actually some lower dimensional representation that models will form where learning occurs.
This is more-or-less what the machine learning principle known as the manifold hypothesis states. Big picture, this explains why models can achieve such high accuracy on naturally occurring data while being unreliable against most input in a mathematical sense. I mentioned this above but, I wanna stress that the manifold structure a model forms occupies an almost negligible fraction of total "volume" in the sense that it's intrinsic dimensionality is far lower than the ambient space around it. We'll talk about this later & it sounds weird now, but models "learn" from the shape and compression of the environment.
We'll take a quick breather because I wanna level-set. I just feel it helps to shine some light on the direction we're about to take. For our purposes, machine learning models are just capturing surface correlation and statistical anomalies of the data. They're not doing anything causal in the sense that they lack true understanding of the concepts they're trained to recognize. Models cannot maintain accuracy against inputs that break these statistical patterns without altering causal relationships. This has lead to an interesting phenomenon known as transferability. As observed in (Papernot et al., 2016), adversarial examples that fool model A will often "transfer" and successfully fool model B, even when these models were trained on different datasets. Models want to study a particular dataset and generalize it to understand the general pattern within that dataset. So it makes sense that these models should more-or-less learn the same thing regardless of which subset of data you train them on. I really want to stress that a model's susceptibility to being tricked by adversarial examples aren't quirks of the model... I'd say its a byproduct of the associative nature of how neural networks learn.
Maybe it's worth mentioning that I like this paper, Ilyas et al., 2019 its logical & argues that if models are trained to maximize accuracy on "real" datasets they will inevitably latch onto any statistically useful pattern that makes them more susceptible to adversarial examples.

You can picture this manifold as a crumpled sheet of paper floating in a huge 3D room. The paper itself is thin and occupies only a tiny fraction of the room's volume. This paper is our manifold and holds all the "real" data the model has learned to recognize and produce.
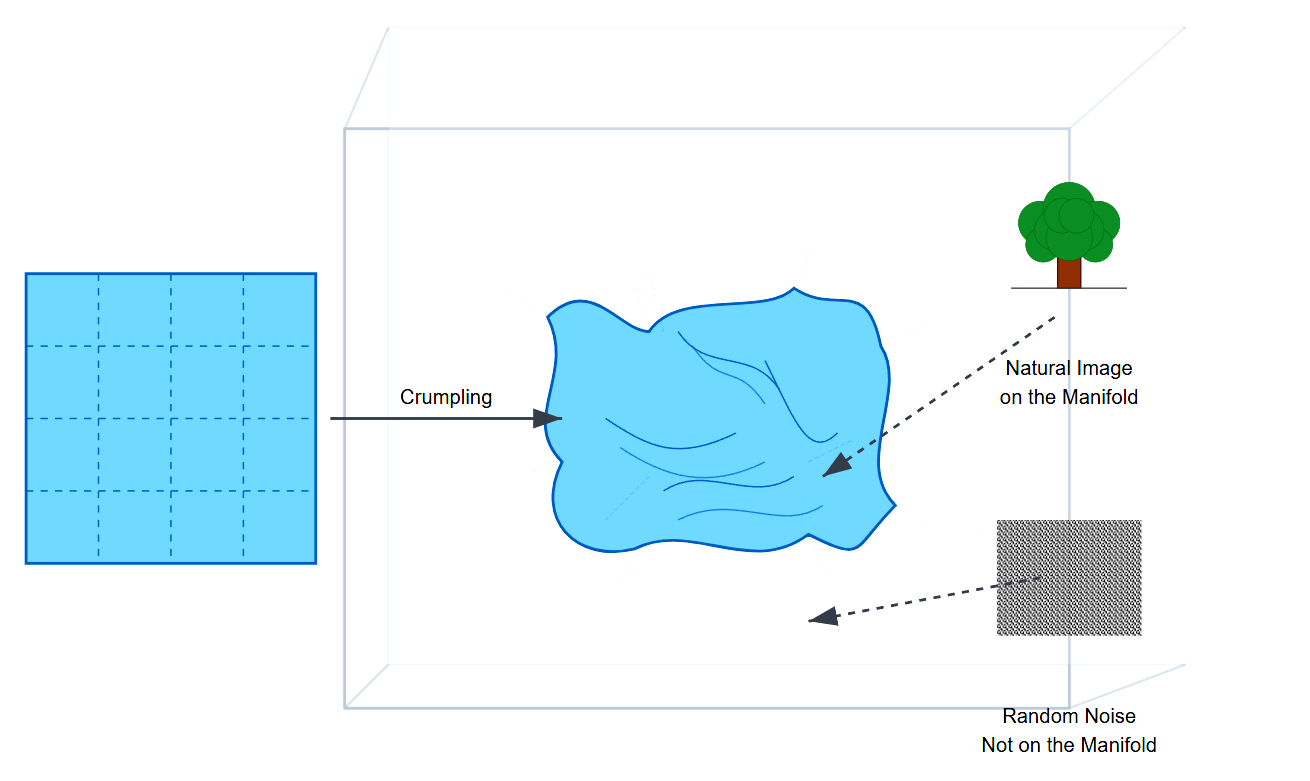
This might help visualize how a manifold's actual dimensionality & it's "degrees of freedom" is way lower than the surrounding space. Models get really good at making predictions on the surface of this crumpled paper but do very poorly against inputs that fall outside the distribution (that vast empty space surrounding it). This makes intuitive sense, right? The model hasn't formed meaningful patterns to work with, so they've got little understanding of the vast regions beyond it. That's why models are wrong across most of the input space (not only in those distribution-free zones). I think this is made worse by a lot of flawed assumptions around independent and identically distributed data (i.i.d) that limit more comprehensive manifold coverage. Limiting this coverage has been found to contribute to hallucinations, which is what happens when models generate fictional outputs in those sparse regions.
The geometry of the manifold not only affects how the model generalizes but also shapes the placement of decision boundaries (the invisible lines that separate different classes in the feature space). These boundaries usually hug close to the data manifold and are tightly aligned with the manifold’s structure (Zhang et al., 2019; Bell et al., 2024; Zhang et al., 2019). Why? The rationale given for this is that if data were generated by some dynamic process that doesn't have a lot of intrinsic degrees of freedom, this fact would be reflected in the geometry of the data. I feel like this makes sense.

There's a lot of other factors at play! But I'd argue that fundamentally, adversarial examples exploit regions where learned representations are absent or incomplete. We'll build on this later in the blog. I also think that the decision boundaries' closeness & the models' tendency to prioritize statistical patterns over deeper causal relationships likely have a significant impact on the success of adversarial examples.
I initially thought this was a generalization problem. And it's kind of is, yet not really. I think the defenses harping on this have shown it likely won't lead to better robustness. There are generalization techniques, such as out-of-distribution detection or generalize within the manifold. From what I've gathered, they're not great & often fall short due to the inherent constraints of the training data's manifold. Fine-tuning "wonky" learned patterns into high-dimensional spaces doesn't perform well. If a model already lacks certain domains like low-resource languages those will always be limiting the model's understanding, which is already tied to the manifold. You're better off figuring out a more comprehensive training strategy than attempting to make models extrapolate its trained manifold. That being said I don't stay up to date with these kinds of "defenses". I'm likely super wrong here. Just mentioning since I spent a few days trying to figure this one out.
Clarification section 😅
The manifold visualized as being crumpled paper implies it is a unified, continuous manifold. This isnt true. For example, natural language manifolds rarely form continuity. They can take on complex shapes & can consist of multiple disconnected regions. Theres a lot of reasons why this might happen. Its not a bad thing per se & can be the result of a model being trained on diverse domains of data, which can cause them to not be perfectly connected on the manifold.
Also the crumpled paper represents the low-dimensional manifold where the model's "knowledge" resides. It's visualized as representing the coherent sentence, concept, or pattern the model understands, which makes up the paper. The model's internal representations (embeddings) are the points on this manifold that capture all learned meaning and context of words or sentences.
I also mentioned that a manifold's geometry may be affected by the generative process and representation of the data a model is trained on. There's an amazing paper on this (Fefferman et al., 2016). Just know the data might not always look like the manifold I visualized.
Lastly, adversarial examples are not necessarily "far from the manifold" in terms of distance. Instead, they are close to the manifold but lie off of it. In most cases, adversarial examples are perturbed in directions perpendicular to the manifold by not a whole lot.
Okay 😮💨... Earlier I said something along the lines of "manifolds occupy an extremely negligible fraction of the full input space". This is a confusing statement. Let's break it down & clarify.
I'm using the term "input space" to refer to the complete volume of all possible inputs that could theoretically be given to a model. For images, think of it as the space of all possible pixel configurations. For language models, it's all possible sequences of tokens. So that's the theoretical input space. Now, the practical input space is effectively limited to a subset of sequences in the training set, which would typically be real-world data (like photos, sounds, or text) which, refering back the the manifold hypothesis, we know isn't scattered randomly throughout this enormous space but instead clusters along a much lower-dimensional manifold.
Consider a 24-megapixel image with 3 colour channels (RGB) and each channel typically has 256 possible values (8 bits). The input space would be 256^(24,000,000×3) of possible pixel configurations. Thats an insanely large number. Obviously, only an insanely tiny fraction of these arrangements form recognizable pictures (pixel arrangements that would look like real things). These "real" images lie on this thin manifold & almost all other arrangements would look like static noise.
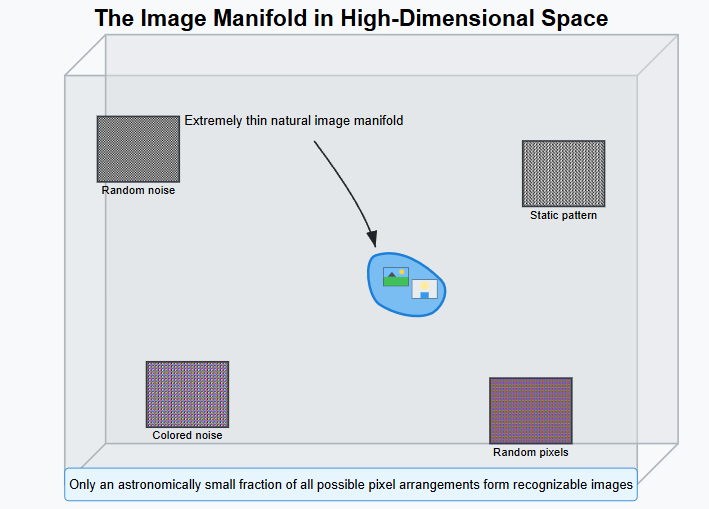
For language models, the input space includes all possible token sequences but only coherent text (grammatically correct sentences) would typically form the manifold (I hate how this sounds). This sparsity where natural data occupies a negligible portion of the input space is what models love & is known as the sparsity principle, which enables them to learn patterns efficiently by focusing on the manifold.
Please remember that this blog is very raw & nobody deep in the academic trenches has picked it apart. My understanding is built from an unhealthy amount of reading. Before it gets called out, a lot of my understanding has been influenced by Shamir et al., 2022. I think it's a solid paper. They figured that during training, models also create decision boundaries in this lower-dimensional space very close to the data manifold. This closeness creates shallow "dimples" that allow the model to create small perturbations to "push" data points across boundaries. I'm not qualified to explain why this happens, but even intuitively this makes sense because you want data to fall on the correct side of training examples while remaining extremely close to the data manifold. Remember, during training you want the decision boundaries to be positioned so that examples from different classes fall on opposite sides of the boundary. I'd also narrowly view this very "push" as another property that adversarial examples exploit.

We saw this in my last blog. As an adversary, you want your adversarial input to be making love to the decision boundary. Thats because you want the minimum confidence score possible that flips you into your target classification you want low confidence and high loss, its a small "push".
There exists other great explanations for adversarial examples, such as Goodfellow et al., 2015 which focus on the linearity of neural networks in high-dimensional spaces. There's also Tanay et al., 2016 which is kinda cool & theorizes that adversarial examples exist because decision boundaries are "tilted" relative to the data distribution. While most papers are complementary, I've focused more on the manifold’s role with respect to the decision boundary’s proximity. I'm sure there are lots of other great research that I simply haven't read.
For better or worse, I think we've learned enough to understand why/how adversarial examples exploit models. To return to our analogy & the manifold hypothesis: models are trained to navigate the paper, not the entire room.
It's also been hypothesized that we might be dealing with an entire room filled with manifolds. Within our context, the input space could be visualized as a room filled with multiple crumpled pieces of paper. Each paper would encode a distinct concept like "Palm" (tree, hand) or "Rock" (stone, music) within the model's feature space. These manifolds represent subsets of the training data that get tied to specific contexts connected by decision boundaries that delineate their boundaries in the high-dimensional space.
This structure may explain how LLMs can differentiate complex concepts but also why adversarial examples succeed. Remember, perturbations can exploit sparse regions or cross boundaries between manifold.
Outside the manifold or even near its boundaries, a model's ability to predict becomes shaky, and yet the model has to predict something. Don't get me wrong, they can predict just fine im more-so harping on coherent instability (coherence doesn’t imply correctness or robustness). Now, with how vast the embedding is, you'll likely always have room to craft images with imperceptible noise or text with subtle rephrasing that exploits these edges. It will likely never be too challenging to nudge input ingested by frontier models just off the crumpled paper, or even near it but across a model's decision boundary.
If I had to boil down everything we've discussed, I'd say the geometry of the data manifold (influenced by sparsity within the high-dimensional input space) is the shaky foundation the models stand on. However, it is the gradients (which guide how inputs are processed) and the decision boundaries (invisible lines separating classes) that closely align with the manifold to separate classes that amplify or suppress the effectiveness of classification. Those are the core elements (including other mentioned above) that enable adversarial examples to exploit a model's limits.
THE END?
Not yet 🙁. Please know that these systems are a lot more complex than I've made them out to be. I've grossly oversimplified certain concepts. There's simply too much to cover in a blog I believe my audience would actually read. IMHO, this is just enough to provide an answer.
If this stuff interests you, there's an entire field of AI research called mechanistic interpretability that focuses on understanding the internal workings of neural networks (especially large language models) at a granular level, reverse-engineering how they process inputs and generate outputs. I'm not talking about traditional interpretability (feature importance); these people are data assassins and do great work mapping things like how neurons or layer encoders handle tasks & produce behaviour.
As I've mentioned before, consider this an informed interpretation & not the final word on the subject. There a lot of very complex interplay between data manifolds & decision boundaries. This is just what makes sense to me & is supported by some reputable research. You should be aware that there can be vast off-manifold regions where model behaviour becomes essentially undefined yet will at the same time reside close to the decision boundaries. I don't know why... it's a rabbit-hole I didnt go down, so beyond assumptions I can't really explain why underrepresented training data can cause the manifold to curve in complex ways that create unexpected proximity between different classes in the feature space...
I know it's shitty not to cover defenses or weave it back to a solution that would prevent your applications from performing misguided actions. I wanna keep my personal blog separate from my job, I have biases, & I don't want to cause any conflicts of interest or get in trouble. Ask me in private & I'll tell you how to protect and have safe LLM applications.
Research and actual products you can implement are very different. Here's some defensive research I've personally liked: Yang et al., 2022, Cohen et al., 2019, and famously Carlini et al., 2023, which introduces Diffusion Denoised Smoothing (DDS). Yet, its my understanding is that DDS reduces the sharpness of decision boundaries which might mitigate the "dimples" effects discussed above? From what I've gathered it mitigates misclassification by making models "wrongness" less exploitable within a certain radius & relies on the base classifier performing well under noise. There's also this awesome paper that just released Debenedetti et al., 2025 that I'd read if I were doing AI red teaming or getting paid for jailbreaks/CTF arenas.
THE END, END 🎉
Thank you for reading! 😅 I hope it wasn't too painful, and maybe you learned something?
I wanna thank my childhood friend (they know who they are) for asking me this question drunk one night. If I hadn't embarrassed myself regurgitating half-baked facts, I likely would have never sought out an actual answer. For the first time since launching boschko.ca, I roped my friends into reviewing this piece. I wanna give a massive thanks to Ads Dawson, Ruikai Peng, and Keith Hoodlet for reading through and offering solid recommendations. This blog would have been a painful read if it weren't for them ❤️.
I hope you liked it! I'm only active on X these days. Follow me there if you want more of these random discoveries and thoughts that keep me up at night.


